
So, we all know that ScyllaDB is a pretty versatile and fast database with lots of potential in the real-time applications, especially ones involving time series. We’ve seen ScyllaDB doing the heavy lifting in the telecom industry, advertising, nuclear research, IoT or banking; this time, however, let’s try something out of the ordinary. How about using ScyllaDB for… numerical calculations? Even better – for distributed numerical calculations? Computations on large matrices require enormous amounts of memory and processing power, and ScyllaDB allows us to mitigate both these issues – matrices can be stored in a distributed cluster, and the computations can be run out-of-place by several DB clients at once. Basically, by treating the ScyllaDB cluster as RAM, we can operate on matrices that wouldn’t fit into a hard disk!
But Why?
Linear algebra is a fundamental area of mathematics that many fields of science and engineering are based on. Its numerous applications include computer graphics, machine learning, ranking in search engines, physical simulations, and a lot more. Fast solutions for linear algebra operations are in demand and, since combining this with NoSQL is an uncharted territory, we had decided to start a research project and implement a library that could perform such computations, using ScyllaDB.
However, we didn’t want to design the interface from scratch but, instead, base it on an existing one – no need to reinvent the wheel. Our choice was BLAS, due to its wide adoption. Ideally, our library would be a drop-in replacement for existing codes that use OpenBLAS, cuBLAS, GotoBLAS, etc.
But what is “BLAS”? This acronym stands for “Basic Linear Algebra Subprograms” and means a specification of low-level routines performing the most common linear algebraic operations — things like dot product, matrix-vector and matrix-matrix multiplication, linear combinations and so on. Almost every numerical code links against some implementation of BLAS at some point.
The crown jewel of BLAS is the general matrix-matrix multiplication (gemm) function, which we chose to start with. Also, because the biggest real-world problems seem to be sparse, we decided to focus on sparse algebra (that is: our matrices will mostly consist of zeroes). And — of course! — we want to parallelize the computations as much as possible. These constraints have a huge impact on the choice of representation of matrices.
Representing Matrices in ScyllaDB
In order to find the best approach, we tried to emulate several popular representations of matrices typically used in RAM-based calculations/computations. Note that in our initial implementations, all matrix data was to be stored in a single database table.
Most formats were difficult to reasonably adapt for a relational database due to their reliance on indexed arrays or iteration. The most promising and the most natural of all was the dictionary of keys.
Dictionary of Keys
Dictionary of keys (or DOK in short) is a straightforward and memory-efficient representation of a sparse matrix where all its non-zero values are mapped to their pairs of coordinates.
CREATE TABLE zpp.dok_matrix (
matrix_id int,
pos_y bigint,
pos_x bigint,
val double,
PRIMARY KEY (matrix_id, pos_y, pos_x)
);NB. A primary key of ((matrix_id, pos_y), pos_x) could be a slightly better choice from the clustering point of view but at the time we were only starting to grasp the concept.
The Final Choice
Ultimately, we decided to represent the matrices as:
CREATE TABLE zpp.matrix_{id} (
block_row bigint,
block_column bigint,
row bigint,
column bigint,
value {type},
PRIMARY KEY ((block_row, block_column), row, column)
);The first visible change is our choice to represent each matrix as a separate table. The decision was mostly ideological as we simply preferred to think of each matrix as a fully separate entity. This choice can be reverted in the future.
In this representation, matrices are split into blocks. Row and column-based operations are possible with this schema but time-consuming. Zeroes are again not tracked in the database (i.e. no values less than a certain epsilon should be inserted into the tables).
Alright, but what are blocks?
Matrix Blocks and Block Matrices
Instead of fetching a single value at a time, we’ve decided to fetch blocks of values, a block being a square chunk of values that has nice properties when it comes to calculations.
Definition:
Let us assume there is a global integer n, which we will refer to as the “block size”. A block of coordinates (x, y) in matrix A = [ a_{ij} ] is defined as a set of those a_{ij} which satisfy both:
(x – 1) * n < i <= x * n
(y – 1) * n < j <= y * n
Such a block can be visualized as a square-shaped piece of a matrix. Blocks are non-overlapping and form a regular grid on the matrix. Mind that the rightmost and bottom blocks of a matrix whose size is indivisible by n may be shaped irregularly. To keep things simple, for the rest of the article we will assume that all our matrices are divisible into nxn-sized blocks.
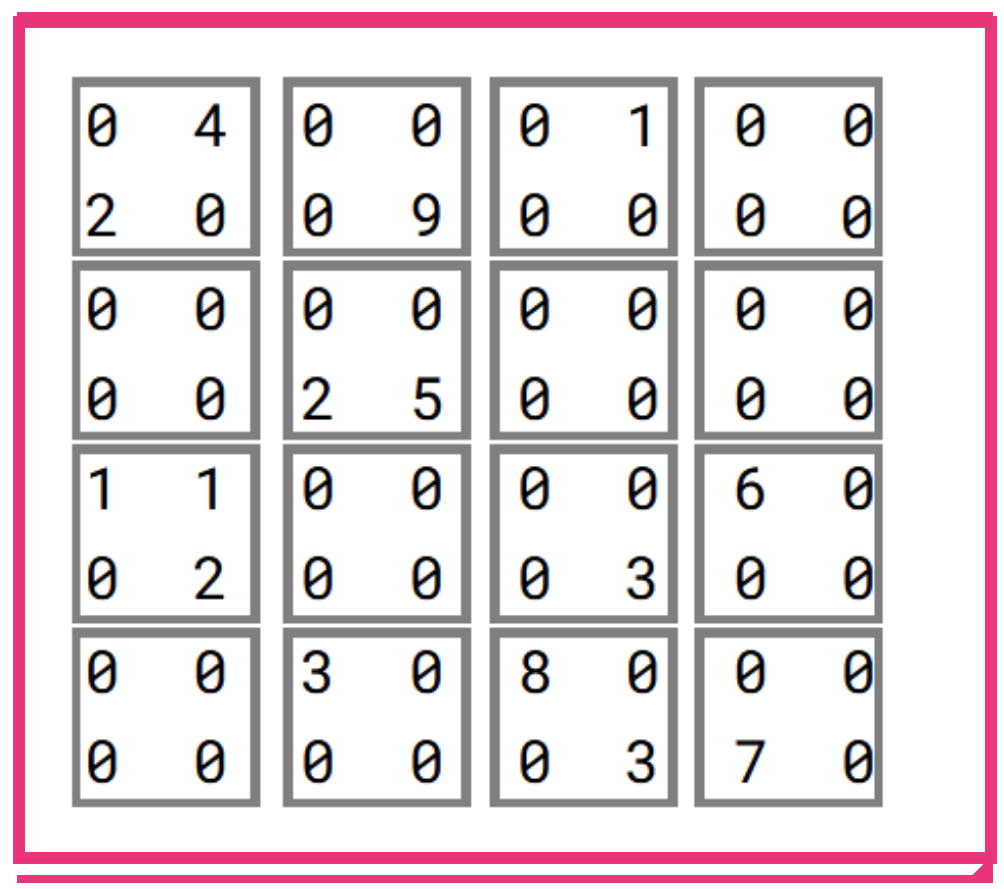
NB. It can easily be shown that this assumption is valid, i.e. a matrix can be artificially padded with (untracked) zeroes to obtain a desired size and all or almost all results will remain the same.
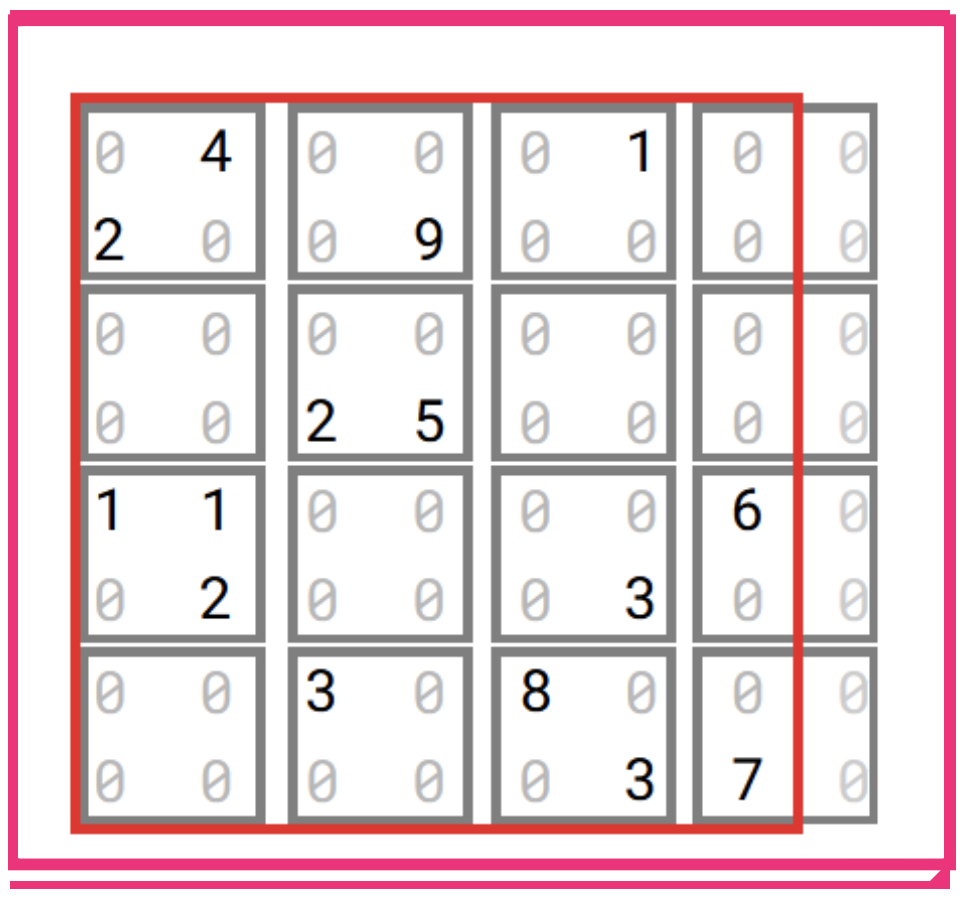
A similar approach has been used to represent vectors of values.
It turns out that besides being good for partitioning a matrix, blocks can play an important role in computations, as we show in the next few paragraphs.
Achieving Concurrency
For the sake of clarity, let us recall the definitions of parallelism and concurrency, as we are going to use these terms extensively throughout the following chapters.
| Concurrency | A condition that exists when at least two threads are making progress. A more generalized form of parallelism that can include time-slicing as a form of virtual parallelism. |
| Parallelism | A condition that arises when at least two threads are executing simultaneously. |
Source:Defining Multithreading Terms (Oracle)
In the operations of matrix addition and matrix multiplication, as well as many others, each cell of the result matrix can be computed independently, as by definition it depends only on the original matrices. This means that the computation can obviously be run concurrently.
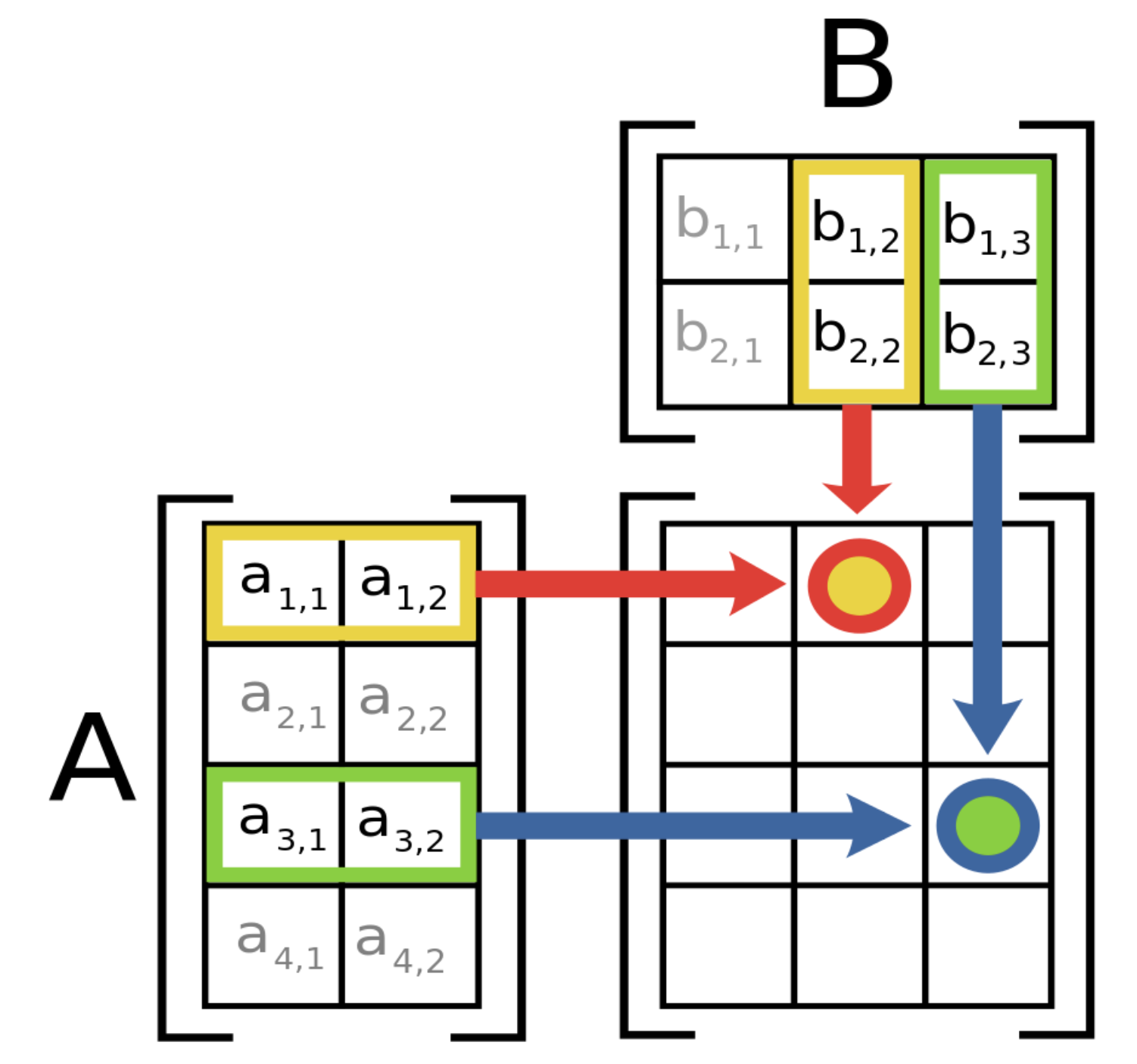
(Matrix multiplication. Source: Wikipedia)
Remember that we are dealing with large, sparse matrices? Sparse – meaning that our matrices are going to be filled mostly with zeroes. Naive iteration is out of question!
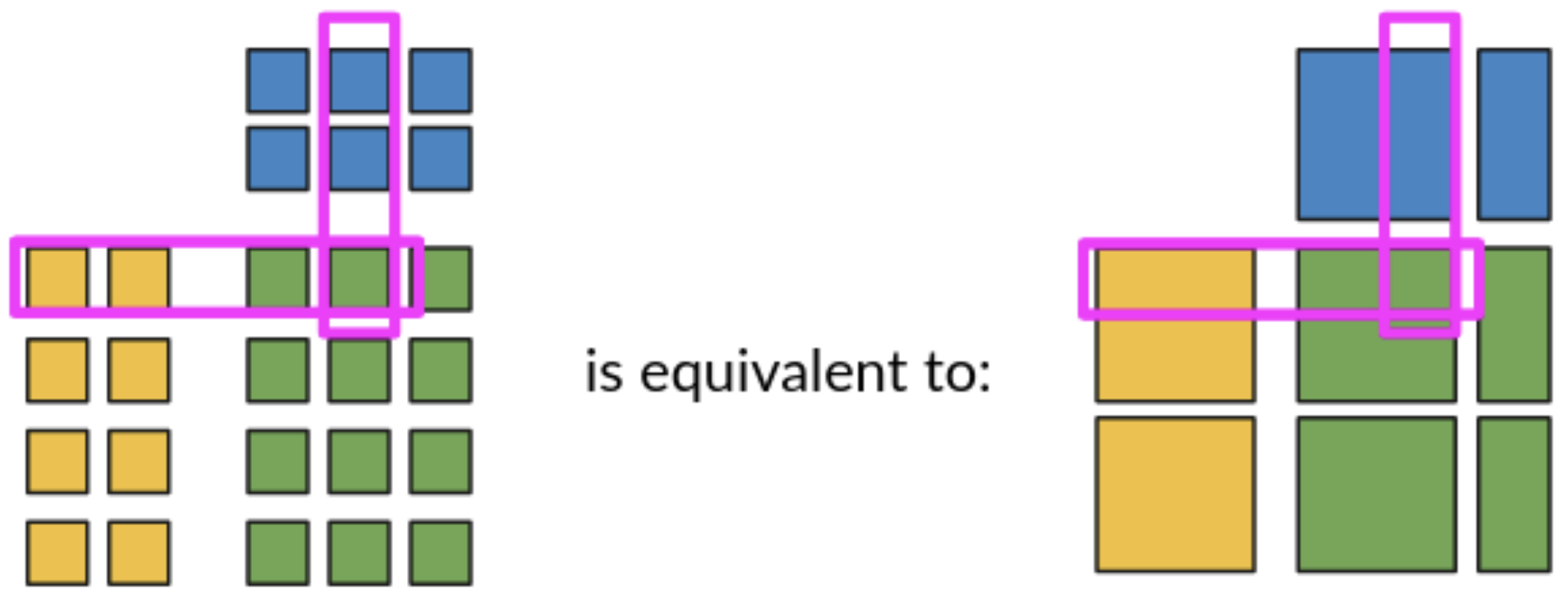
It turns out that bulk operations on blocks give the same results as direct operations on values (mathematically, we could say that matrices of values and matrices of blocks are isomorphic). This way we can benefit from our partitioning strategy, downloading, computing and uploading entire partitions at once, rather than single values, and performing computation only on relevant values. Now that’s just what we need!
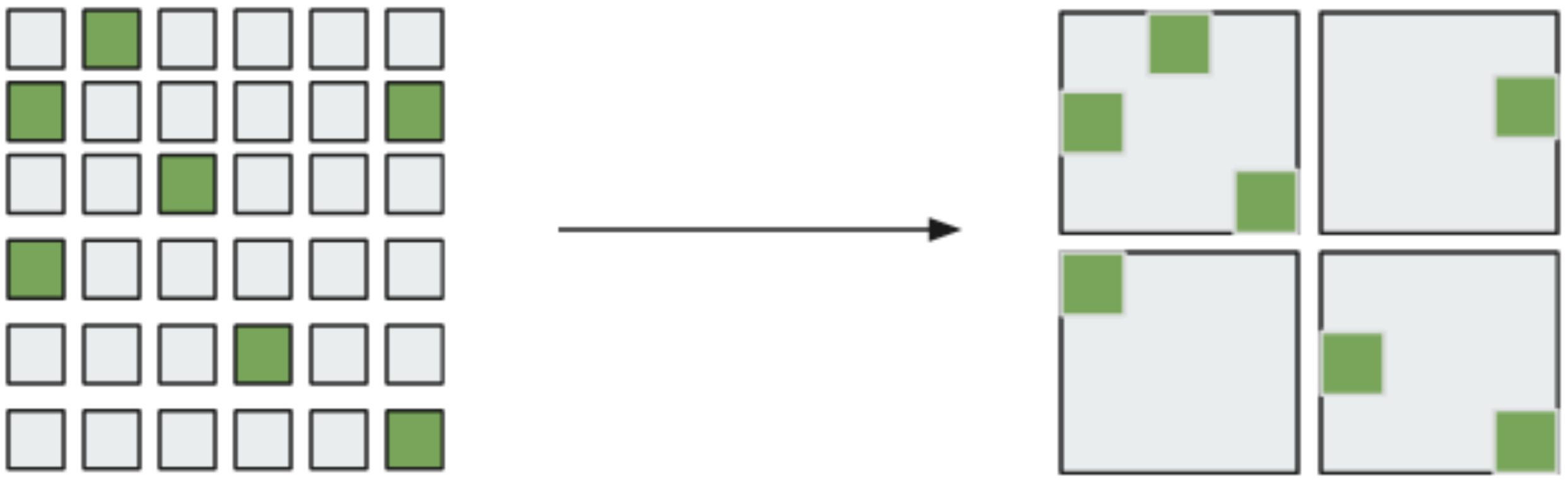
Parallelism
Let’s get back to matrix multiplication. We already know how to perform the computation concurrently: we need to use some blocks of given matrices (or vectors) and compute every block of the result.
So how do we run the computations in parallel?
Essentially, we introduced three key components:
- a scheduler
- ScyllaDB-based task queues
- workers
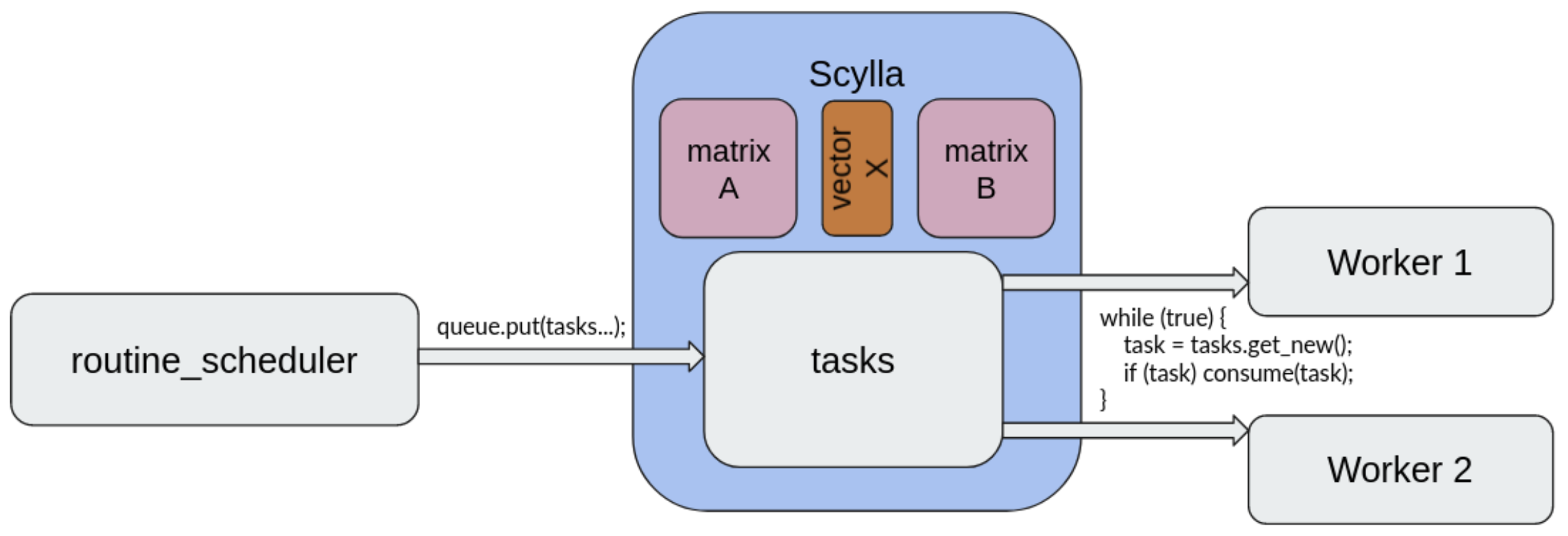
To put the idea simply: we not only use ScyllaDB to store the structures used in computations, but also “tasks”, representing computations to be performed, e.g. “compute block (i, j) of matrix C, where C = AB; A and B are matrices”. A worker retrieves one task at a time, deletes it from the database, performs a computation and uploads the result. We decided to keep the task queue in ScyllaDB solely for simplicity: otherwise we would need a separate component like Kafka or Redis.
The scheduler is a class exposing the library’s public interface. It splits the mathematical operations into tasks, sends them to the queue in ScyllaDB and monitors the progress signaled by the workers. Ordering multiplication of two matrices A and B is as simple as calling an appropriate function from the scheduler.
As you may have guessed already, workers are the key to parallelisation – there can be arbitrarily many of them and they’re independent from each other. The more workers you can get to run and connect to ScyllaDB, the better. Note that they do not even have to operate all on the same machine!
A Step Further
With the parallelism in hand we had little to no problem implementing most of BLAS operations, as almost every BLAS routine can be split into a set of smaller, largely independent subproblems. Of all our implementations, the equation system solver (for triangular matrices) was the most difficult one.
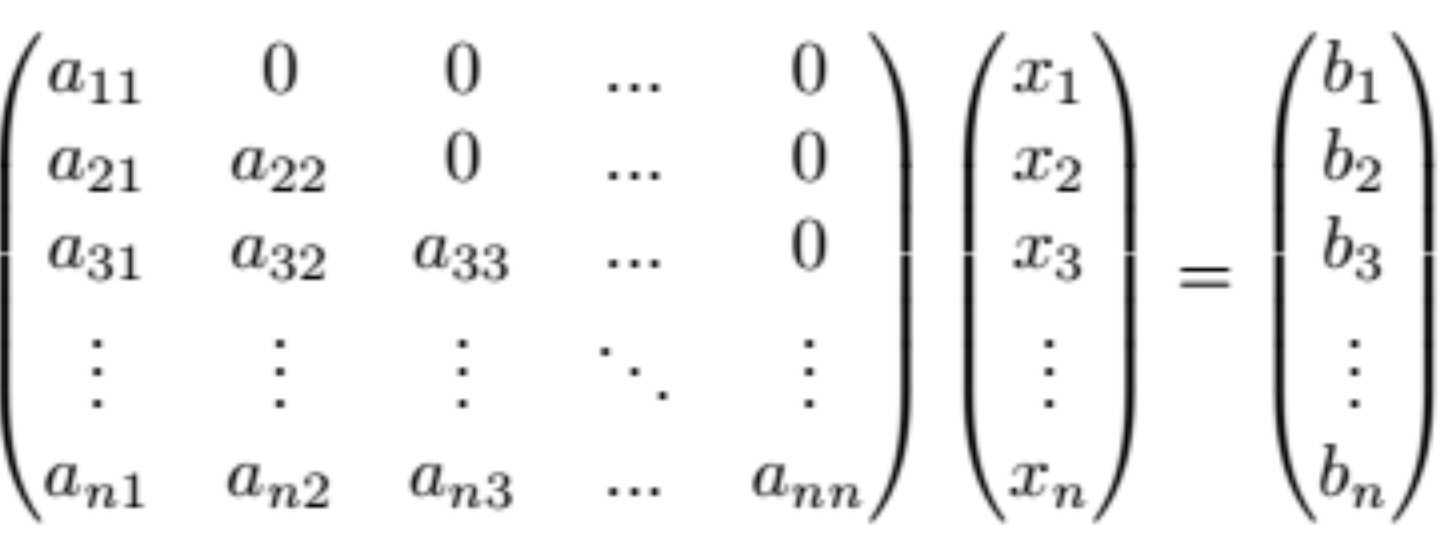
Normally, such systems can easily be solved iteratively: each value bi of the result can be computed based on the values ai1, …, aii, x1, …, xi-1 and bi. as
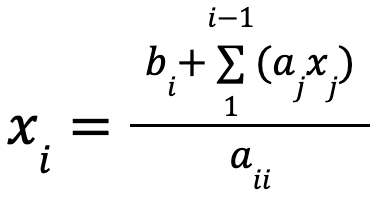
This method doesn’t allow for concurrency in the way we described before.
Conveniently, mathematicians have designed different methods of solving equation systems, which can be run in parallel. One of them is the so-called Jacobi method, which is essentially a series of matrix-vector multiplications repeated until an acceptable result is obtained.
One downside of this approach is that in some cases this method may never yield an acceptable result; fortunately for us, this shouldn’t happen too often for inputs representing typical real-life computational problems. The other is that the results we obtain are only (close) approximations of the exact solutions. We think it’s a fair price for the benefit of scalability.
Benchmarks
To measure the efficiency of our library, we performed benchmarks on the AWS cloud.
Our test platform consisted of:
- Instances for workers – 2 instances of c5.9xlarge:
- 2 × (36 CPUs, 72GiB of RAM)
- Running 70 workers in total.
- Instances for ScyllaDB – 3 instances of i3.4xlarge:
- 3 × (16CPUs, 122GiB of RAM, 2×1,900GB NVMe SSD storage)
- Network performance of each instance up to 10 Gigabit.
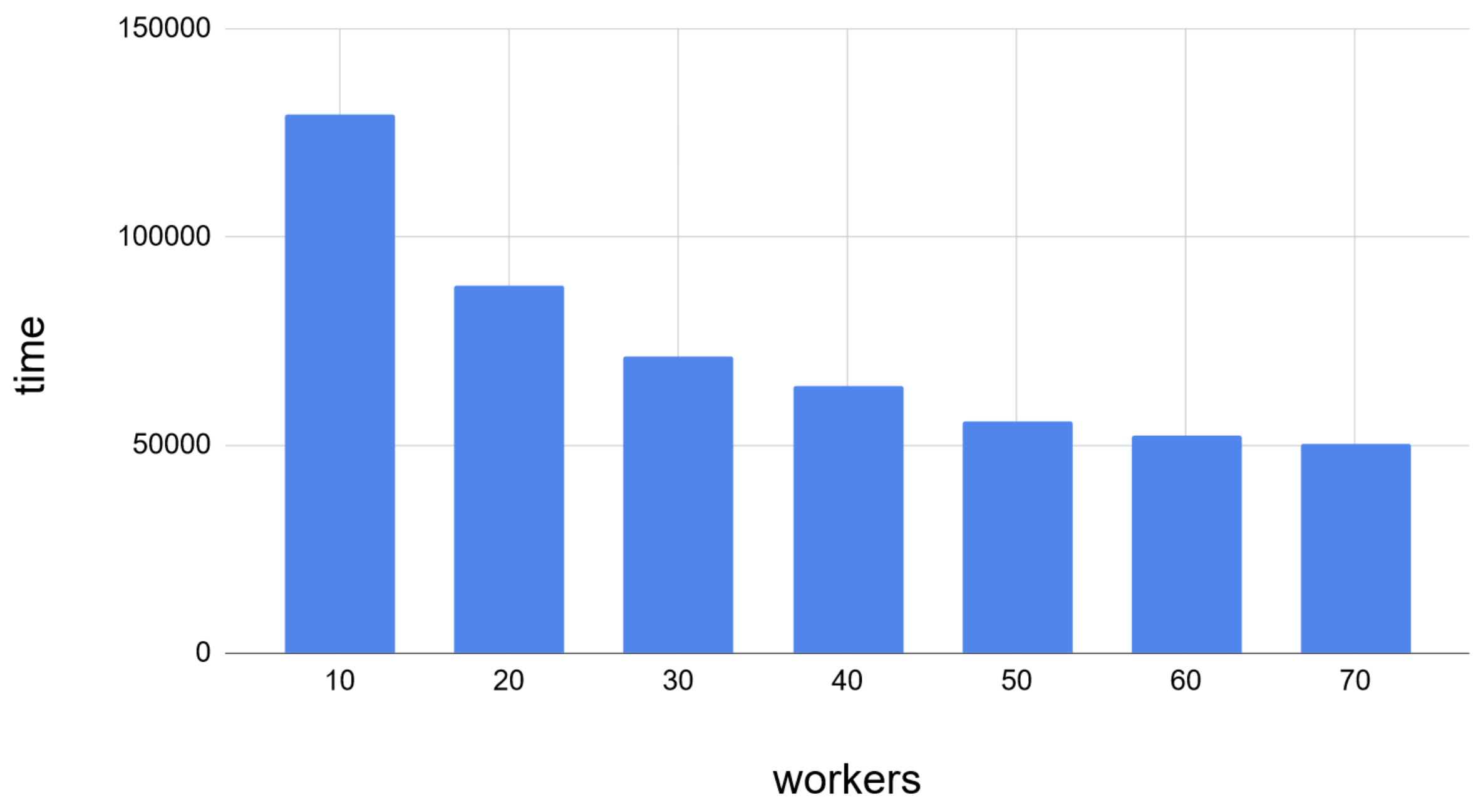
We have tested matrix-matrix multiplication with a variable number of workers.
The efficiency scaled well, at least up to a certain point, where database access became the bottleneck. Keep in mind that in this test we did not change the number of ScyllaDB’s threads.
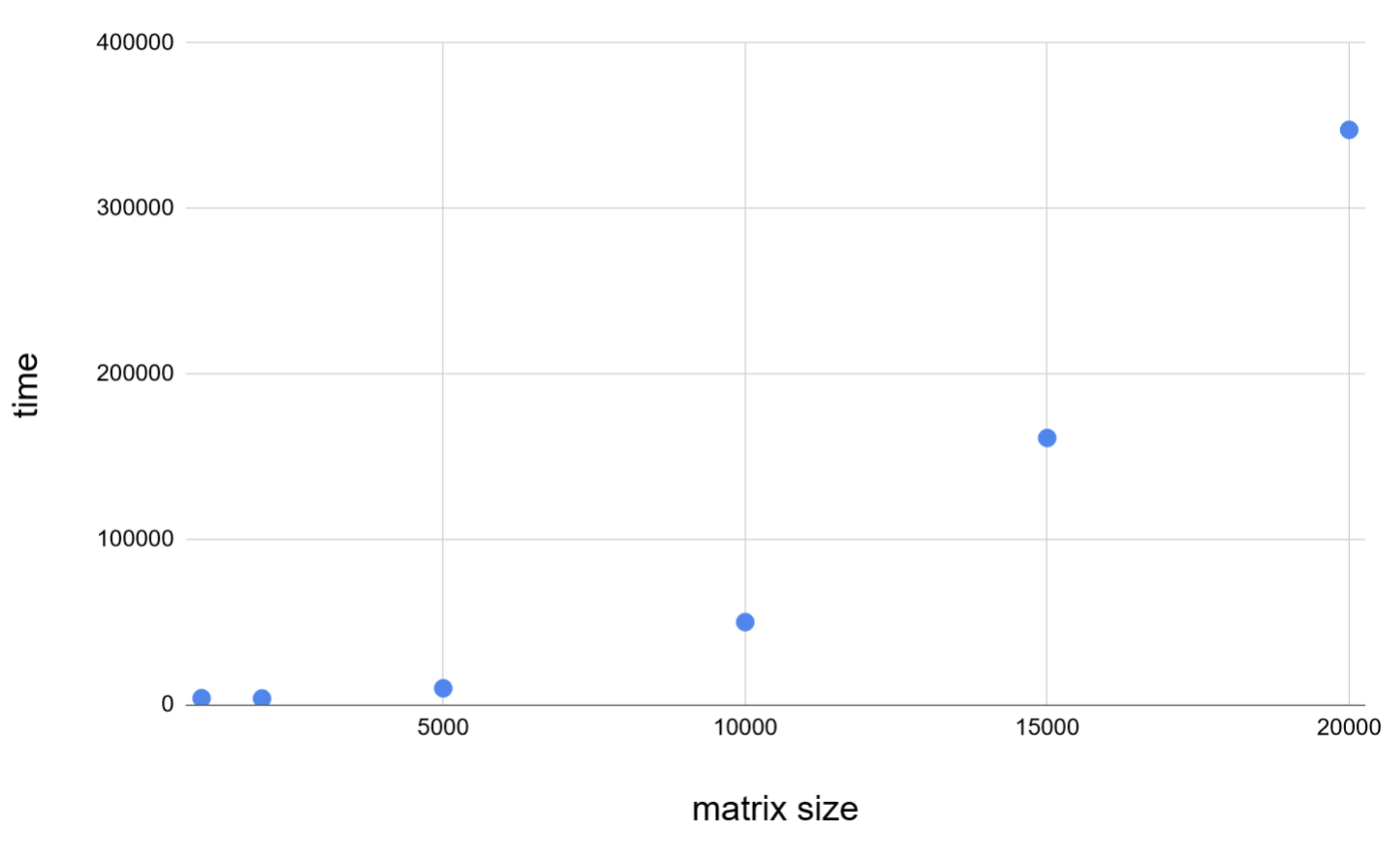
Matrix-matrix multiplication (gemm), time vs input size. Basic gemm implementations perform O(n3) operations, and our implementation does a good job of keeping the same time complexity.
Our main accomplishment was a multiplication of a big matrix (106×106, with 1% of the values not being 0) and a dense vector of length 106.
Such a matrix, stored naively as an array of values, would take up about 3.6TiB of space whereas in a sparse representation, as a list of <block_x, block_y, x, y, value>, it would take up about 335GiB.
The block size used in this example was 500*500. The test concluded successfully – the calculations took about 39 minutes.
Something Extra: Wrapper for cpp-driver
To develop our project we needed a driver to talk to ScyllaDB. The official scylla-cpp-driver (https://github.com/scylladb/cpp-driver), despite its name, only exposes C-style interface, which is really unhandy to use in modern C++ projects. In order to avoid mixing C-style and C++-style code we developed a wrapper for this driver, that exposes a much more user-friendly interface, thanks to usage of RAII idiom, templates, parameter packs, and other mechanisms.
Wrapper’s code is available at https://github.com/scylla-zpp-blas/scylla_modern_cpp_driver.
Here is a short comparison of code required to set up a ScyllaDB session. On the left cpp-driver, on the right our wrapper.

Summary
This research project was jointly held between ScyllaDB and the University of Warsaw, Faculty of Mathematics, Informatics and Mechanics, and constituted the BSc thesis for the authors. It was a bumpy but fun ride and ScyllaDB did not disappoint us: we built something so scalable that, although still being merely a tidbit, could bring new quality to the world of sparse computational algebra.
The code and other results of our work are available for access at the GitHub repository:
https://github.com/scylla-zpp-blas/linear-algebra
No matter whether you do machine learning, quantum chemistry, finite element method, principal component analysis or you are just curious — feel free to try our BLAS in your own project!



